2.3. Tratamiento de valores atípicos#
Introducción#
Los datos con ruido (noisy data) y valores atípicos (outliers values), son conceptos diferentes, que generalmente se detectan visualmente y/o con técnicas estadísticas.
Por un lado, los datos con ruido representan errores en los datos, que pueden surgir debido a un mal funcionamiento de un sensor, un dato mal ingresado por el usuario, etc.
Por otro lado, los valores atípicos son valores que caen lejos de la mayoría de los valores existentes, por ejemplo, un sensor de temperatura que marque 35°C en invierno en Neuquén. Un valor atípico puede ser válido o puede ser un error (noisy).
Cualquiera sea el caso, se deben analizar e implementar mecanismos para detectarlos y luego eliminarlos o corregirlos. Dejar este tipo de valores en los datos pueden afectar los resultados de los análisis.
Identificación de valores atípicos#
El primer paso para analizar la existencia de valores atípicos en los datos es la identificación de los mismos como tales. En este caso la visualización es una de las herramientas más comunes para identificarlos ya que brindan una visión clara de la distribución de los datos.
Vamos a agregar la siguiente librería:
Matplotlib: para crear visualizaciones estáticas, animadas e interactivas en Python.
Hay diferentes gráficos que podemos utilizar para visualizar estos valores. Veremos algunos de ellos.
Comenzamos creando un
dataframecon diferentes datos:
#importamos las librerías que vamos a utilizar
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
datos = {'Peso': [50.6, 76.9, 45.8, 78.2, 67.9, 85.8, 43.6, 98.7, 283.8, 65.9, 48]}
df_pesos = pd.DataFrame(datos)
df_pesos
| Peso | |
|---|---|
| 0 | 50.6 |
| 1 | 76.9 |
| 2 | 45.8 |
| 3 | 78.2 |
| 4 | 67.9 |
| 5 | 85.8 |
| 6 | 43.6 |
| 7 | 98.7 |
| 8 | 283.8 |
| 9 | 65.9 |
| 10 | 48.0 |
Diagramas de dispersión#
Para hacer el gráfico de dispersión (scatter plot) hay dos métodos principales:
plt.subplots: que permite crear una figura y uno o más ejes (subgráficos) dentro de la misma. Por ejemplo:fig, ax = plt.subplots(figsize=(10,4))define afigcomo la figura,axun subgráfico o área donde se dibujan los datos, yfigsizeel parámetro para indicar el tamaño de la misma.ax.scatter(x,y): dondexrepresenta los valores deleje x,ylos valores que debe tomar eleje yy se define para el área creada (ax).
Para graficar los pesos de las personas de
df_pesoshacemos:
#comenzamos enviando datos para la configuración del grafico
#Defino el tamaño del grafico
fig, ax = plt.subplots(figsize=(10,4))
# Agrego etiquetas para eje x, eje y y titulo
plt.xlabel("Rango de Pesos")
plt.ylabel("Pesos")
# Le agrego la leyenda del titulo
plt.title("Diagrama para los pesos")
#la funcion scatter toma como primer parámetro el eje x
# que es la cantidad de pesos registrados, en este caso el rango de 0 a 13
# y el eje y que es la columna de pesos
ax.scatter(x=range(len(df_pesos['Peso'])), y=df_pesos['Peso'])
# podemos guardar la figura generada en la carpeta archivosGenerados/
plt.savefig("archivosGenerados/ScatterPesos.png")
plt.show()
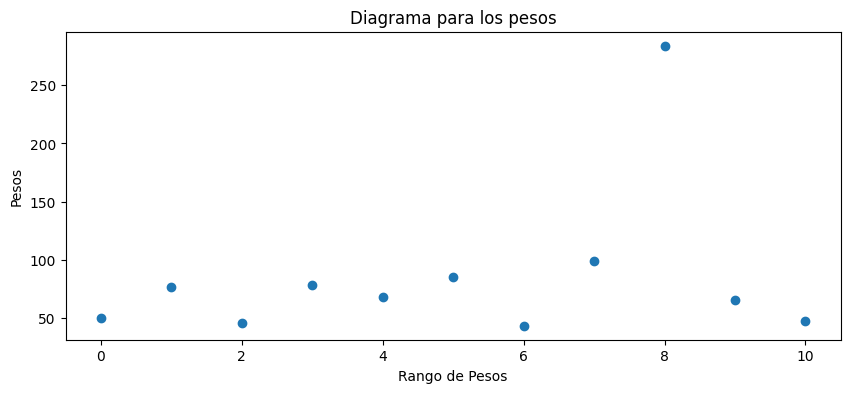
Como podemos observar en el diagrama el valor de 283.8 parece un valor atípico, aunque podría ser real.
Rango Intercuartílico (IQR)#
Existen variables importantes que nos permiten analizar la distribución de los datos e identificar valores atípicos.
Variables importantes
Las variables mas importantes a calcular a la hora de buscar atípicos son:
mediana: valor del medio (impar) o promedio de los dos valores centrales (par)
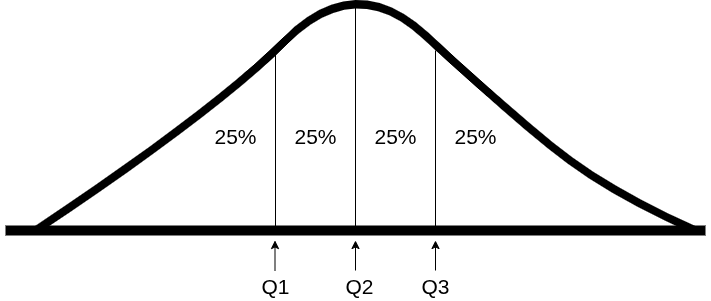
cuartiles: división de los datos en 4 partes iguales, cada una con el 25%:
Q1: Es el valor a partir del cual tengo el 25% de los datos por debajo y el 75% por arriba. También se llama cuartil inferior.
Q2: Es la mediana, es decir el valor a partir del cual el 50% de los datos están por debajo y por arriba.
Q3: Es el valor a partir del cual el 75% de los datos están por debajo y el 25% por arriba.
En el grafico siguiente podemos ver estos valores en una distribución normal:
Vamos primero a ordenar
df_pesospara ver como son los datos:
#primero ordenamos los pesos para conocerlos
# tambien se podria haber hecho como {df_pesos["Peso"].sort_values()} que devuelve una serie
df_pesos.sort_values(by='Peso', ascending=True)
| Peso | |
|---|---|
| 6 | 43.6 |
| 2 | 45.8 |
| 10 | 48.0 |
| 0 | 50.6 |
| 9 | 65.9 |
| 4 | 67.9 |
| 1 | 76.9 |
| 3 | 78.2 |
| 5 | 85.8 |
| 7 | 98.7 |
| 8 | 283.8 |
Vamos ahora a calcular los cartiles de los datos de los pesos de
df_pesos:
# calculo el primer cuartil (25%)
q1 = np.quantile(df_pesos['Peso'], 0.25)
print(f'El primer cuartil Q1 (25%) es {q1}')
# calculo el segundo cuartil (50% o mediana)
q2 = np.quantile(df_pesos['Peso'], 0.50)
print(f'El segundo cuartil Q2 (mediana) (50%) es {q2}')
# calculo el tercer cuartil (75%)
q3 = np.quantile(df_pesos['Peso'], 0.75)
print(f'El tercer cuartil Q3 (75%) es {q3}')
El primer cuartil Q1 (25%) es 49.3
El segundo cuartil Q2 (mediana) (50%) es 67.9
El tercer cuartil Q3 (75%) es 82.0
Otra variable importante de entender para graficar la dispersión de los datos es el rango intercuartil (IQR).
Rango Intercuartil (IQR)
El IQR es la distancia entre el primer (Q1) y el tercer cuartil (Q3) indicando la dispersión media de los datos, es decir, sólo incluye el 50% medio de los datos. De esta forma no se afectado por valores extremos.
IQR = Q3 - Q1
Calculando manualmente el IQR:
# calculo el iqr
iqr = q3-q1
print(f'El IQR es {iqr}')
El IQR es 32.7
Debido a que Q1 , la mediana y Q3 juntos no contienen información sobre los puntos finales de los datos, se puede obtener un resumen más completo de la forma de una distribución al proporcionar también los valores de datos más bajos y más altos. Esto se conoce como el resumen de cinco números:
mediana (Q2),
Q1,
Q3 ,
valor minimo, el menor valor del conjunto de datos,
valor_maximo, el mayor valor del conjunto de datos
Límites mínimo y máximo
Una regla general común para identificar valores atípicos sospechosos es seleccionar valores que caigan en al menos 1,5 × IQR por encima del tercer cuartil (Q3) o por debajo del primer cuartil (Q1).
Entonces, se definen dos valores más como:
limite máximo = Q3 + 1,5 × IQR
limite mínimo = Q1 - 1,5 × IQR
Vamos primero a calcular, con nuestros datos, los valores de los límites mínimo y máximo:
## Calculamos el limite maximo para el cual los valores mayores a ese
# son considerados outliers
limite_max = q3+(1.5*iqr)
print(f'El limite máximo es: {limite_max}')
## Calculamos el limite mínimo para el cual los valores menores a ese
# son considerados outliers
limite_min = q1-(1.5*iqr)
print(f'El limite mínimo es: {limite_min}')
El limite máximo es: 131.05
El limite mínimo es: 0.2499999999999929
El resultado significa que los valores mas grandes que 131.05 y menores a 0.249 serán considerados atípicos.
Diagramas de cajas#
Otro gráfico útil y generalmente utilizado para graficar valores atípicos son los diagramas de caja (boxplot).
Diagramas boxplot
Los boxplot grafican según el resumen de cinco números de la siguiente forma:
En los extremos de la caja están los cuartiles, de modo que la longitud de la caja es justamente el IQR.
La mediana está marcada por una línea dentro de la caja (Q2).
Q1 es el valor inferior donde comienza de la caja.
Q3 es el valor superior donde termina la caja.
Dos líneas (llamadas bigotes) fuera de la caja que se extienden hasta las observaciones más bajas (valor minimo) y más altas (valor maximo), que no son consideradas atípicas según la regla del IQR:
bigote inferior es el valor mas chico de los datos, pero mayor al limite mínimo
bigote superior es el valor mas alto de los datos, pero menor al limite máximo
En la figura lo podemos observar los valores (en una distribución normal):

El gráfico de los diagramas de caja (boxplot) se realiza con el método ax.boxplot() donde se le envía como parámetro la serie (columna) a graficar.
Graficamos el boxplot con los valores calculados:
#Defino el tamaño del grafico
fig, ax = plt.subplots(figsize=(2, 8))
# Agrego etiquetas para eje x, eje y y titulo
plt.xlabel("Pesos")
plt.ylabel("Medidas")
# para indicar que valores me muestre en el eje x o y, se usa xticks o yticks
# definimos para el eje y
#desde 40 hasta 301 de 10 en 10
plt.yticks(np.arange(40, 301, 5))
# Le agrego la leyenda del titulo
plt.title("Boxplot para los pesos")
ax.boxplot(df_pesos['Peso'])
# podemos guardar la figura generada
plt.savefig("archivosGenerados/BoxPlotPesos.png")
#la mostramos
plt.show()

Como podemos observar en el gráfico tenemos los valores:
Q1 (borde inferior de la caja) = 49.3
Q2 (linea en naranja en la caja) = 67.9
Q3 (borde superior de la caja) = 82
valor minimo = 43.6
valor maximo = 98.7
Histogramas#
Por último lo podemos graficar en un diagrama de histogramas el cual muestra la distribución de frecuencias de un conjunto de datos, es decir, agrupa los datos en intervalos (llamados “bins”) y muestra cuántos valores caen en cada intervalo.
Histogramas
Los histogramas se componen de:
eje X: los intervalos de valores (bins).
eje Y: la frecuencia (cantidad de datos) en cada intervalo.
Barras: representan la cantidad de datos dentro de cada bin.
Un dato importante es indicar el número de bins deseado. El mismo se utiliza para dividir el rango de datos en esa cantidad de intervalos de igual tamaño.
Por lo tanto, al construir un histograma debemos: (1) indicar el rango de datos en intervalos (bins), (2) contar cuántos datos caen en cada bins y (3) dibujar una barra para cada uno cuya altura es su frecuencia. Por suerte python lo hace solito!
Recordemos nuestros datos ordenados:
df_pesos.sort_values(by='Peso')
| Peso | |
|---|---|
| 6 | 43.6 |
| 2 | 45.8 |
| 10 | 48.0 |
| 0 | 50.6 |
| 9 | 65.9 |
| 4 | 67.9 |
| 1 | 76.9 |
| 3 | 78.2 |
| 5 | 85.8 |
| 7 | 98.7 |
| 8 | 283.8 |
Para construir el histograma hay que enviarle como parámetro el número de bins. En nuestro ejemplo df_pesos['Peso'] tenemos datos que van desde 43.6 a 283.8, entonces el ancho se define como el valor_maximo-valor_minimo (283.8 - 43.6 = 240.2) y luego ese dato dividido la cantidad de bins=5 (48.04), entonces ancho = (valor_maximo-valor_minimo)/bins.
Note que estos valores no son los mismos que los definidos en el boxplot.
Para comprender el funcionamiento general del diagrama y la construcción de los bins, podemos definir manualmente los bordes como:
Primer borde: 43.6 (valor mínimo en los datos)
Segundo borde: 43.6 + 48.04 (ancho) = 91.64
Tercer borde: 91.64 + 48.04 (ancho) = 139.68
Cuarto borde: 139.68 + 48.04 (ancho) = 187.72
Quinto borde: 187.72 + 48.04 (ancho) = 235.76
Sexto borde: 235,76 + 48.04 (ancho) = 283.8 (valor máximo en los datos)
Entonces cada bins se compone de:
bins1: datos de 43.6 a 91.64
bins2: datos de 91.64 a 139.68
bins3: datos de 139.68 a 187.72
bins4: datos 187.72 a 235.76
bins5: datos 235.76 a 283.8
Como podemos observar 9 datos entran en el bins1, 1 solo en el bins2, los demas estan vacios, y luego solo 1 en el bins5.
Para graficar el histograma podemos obtener los valores de cada borde y la cantidad de datos en cada bins según el método hist().
Graficamos el histograma con nuestros datos de los pesos:
#Defino el tamaño del grafico
fig, ax = plt.subplots(figsize=(5, 5))
nbins=5
# Agrego etiquetas para eje x, eje y y titulo
plt.xlabel("Pesos")
plt.ylabel("Frecuencia (cantidad e datos en cada bins)")
# Creo el histograma y obtengo el valor de cada borde (bordes) generado automáticamente
# y la cantidad de valores en cada uno.
# el guion bajo en el siguiente comando significa "obviar" los valores de la respuesta
# que no quiero usar.
cantidad, bordes, _ = plt.hist(df_pesos['Peso'], bins=nbins, color='skyblue', edgecolor='black')
# Muestro en el hist los bordes en el eje x, nuevamente con xticks
# borde:.2f, el 2f hace que muestre solo 2 decimales de los numeros
plt.xticks(bordes, labels=[f"{borde:.2f}" for borde in bordes])
# y para el eje y tambien lo configuro
#desde 0 hasta 10 de 1 en 1
plt.yticks(np.arange(0, 10, 1))
# Le agrego la leyenda del titulo
plt.title("Histogramas para los pesos")
# podemos guardar la figura generada
plt.savefig("archivosGenerados/HistPesos.png")
#la mostramos
plt.show()
# imprimo los valores para conocerlos
print(f'''Para {nbins} bins, los bordes que definió el método hist() son {bordes}
y la cantidad de datos en cada uno es {cantidad}''')
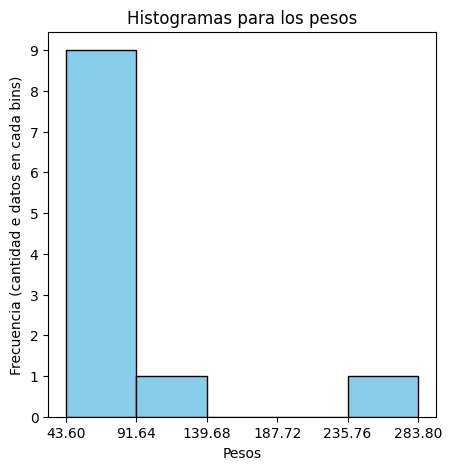
Para 5 bins, los bordes que definió el método hist() son [ 43.6 91.64 139.68 187.72 235.76 283.8 ]
y la cantidad de datos en cada uno es [9. 1. 0. 0. 1.]
A su vez, podemos calcular los bordes de cada bins y los valores que caen en cada uno utilizando otros métodos como cut() de Pandas. Este método agrupa los valores numéricos en rangos de acuerdo a la cantidad enviada como parámetro.
Para el caso de los pesos, usamos
cut()con 5 bins:
numero_bins = 5
# Crear bins que es una serie
bins = pd.cut(df_pesos['Peso'], bins=numero_bins)
#bins.dtype
bins
0 (43.36, 91.64]
1 (43.36, 91.64]
2 (43.36, 91.64]
3 (43.36, 91.64]
4 (43.36, 91.64]
5 (43.36, 91.64]
6 (43.36, 91.64]
7 (91.64, 139.68]
8 (235.76, 283.8]
9 (43.36, 91.64]
10 (43.36, 91.64]
Name: Peso, dtype: category
Categories (5, interval[float64, right]): [(43.36, 91.64] < (91.64, 139.68] < (139.68, 187.72] < (187.72, 235.76] < (235.76, 283.8]]
Como podemos observar en el listado, de los 11 valores de las edades, clasifica cada uno en un bins diferente, por eso devuelve 11 valores. Podemos observar también que los intervalos de los bins no fueron exactamente iguales que para hist(), esto se debe a la forma en que cada método crea el _ bins_. La información de la forma que que cut() crea el bins y sus parámetros, puede encontrarse aca.
Si ahora los queremos agrupar por valor único y contar, podemos usar el método value_counts() que jusyamente cuenta cuántas veces aparece cada valor distinto en la serie.
Usamos
value_counts()para conocer la cantidad de valores en cada bins:
# Contar cuántos datos caen en cada bin
cuantos_datos = bins.value_counts().sort_index()
cuantos_datos
Peso
(43.36, 91.64] 9
(91.64, 139.68] 1
(139.68, 187.72] 0
(187.72, 235.76] 0
(235.76, 283.8] 1
Name: count, dtype: int64
Eliminación o reemplazo de atípicos#
En esta parte vamos sólo a mostrar como eliminar o reemplazar los valores atípicos.
Probamos borrar los valores atípicos, que son aquellos que cayeron mas alla del
limite_maxylimite_minque calculamos previamente:
# crear un nuevo df que posea los
# pesos que cayeron antes del limite_max
df_pesos_sin_atipicos = df_pesos.loc[df_pesos['Peso']< limite_max,['Peso']]
#ordenos
df_pesos_sin_atipicos.sort_values(by = 'Peso')
| Peso | |
|---|---|
| 6 | 43.6 |
| 2 | 45.8 |
| 10 | 48.0 |
| 0 | 50.6 |
| 9 | 65.9 |
| 4 | 67.9 |
| 1 | 76.9 |
| 3 | 78.2 |
| 5 | 85.8 |
| 7 | 98.7 |
Además de borrarlos, podriamos reemplazarlos por la mediana, media, o valores determinados.
Reemplazamos atípicos por la mediana:
# busco la mediana que la teniamos en q2
#hago una copia primero
df_pesos_sin_atipicos2 = df_pesos.copy()
#print(df_pesos_sin_atipicos2)
#busco el valor atipico, como puede ser mas de uno se guarda en un df_atipico
df_atipico = df_pesos.loc[df_pesos['Peso']> limite_max, ['Peso']]
#print(f'Los valores atípicos son: \n{df_atipico}')
#itero sobre el df_atipico
for i in range(len(df_atipico)):
#tomo el primer valor, y lo busco en todo el df_pesos_sin_atipicos para reemplazar
#print(valor_atipico)
valor_atipico = df_atipico.iloc[i]['Peso']
#tambien funcionaba como
#df_pesos_sin_atipicos2.loc[:,'Peso'].replace(valor_atipico,q2)
df_pesos_sin_atipicos2 = df_pesos_sin_atipicos2.replace(valor_atipico,q2)
df_pesos_sin_atipicos2
| Peso | |
|---|---|
| 0 | 50.6 |
| 1 | 76.9 |
| 2 | 45.8 |
| 3 | 78.2 |
| 4 | 67.9 |
| 5 | 85.8 |
| 6 | 43.6 |
| 7 | 98.7 |
| 8 | 67.9 |
| 9 | 65.9 |
| 10 | 48.0 |
